Couplage Multiphysiques

Nos travaux dans ce thème ont pour objet la caractérisation, la modélisation et la simulation de couplages multiphysiques pour différents types de matériaux (métalliques, céramiques et polymères/élastomères) et différents domaines d’applications. Nous nous intéressons plus particulièrement au développement de modèles comportements ou de méthodes numériques originales adaptées à ce contexte multiphysique.

Participants permanents : Djaffar Boussaa (CR), Thierry Désoyer (Prof ECM), Dominique Eyheramendy (Prof ECM), Frédérique Lebon (Prof AMU), Stéphane Lejeunes (IR), Laurent Sabatier (IR)

Modélisation et caractérisation de comportement couplés

Il s’agit de problématiques ou la mécanique est couplée à plusieurs physiques (thermique, chimie, électro-magnétisme, etc) dans un cadre non-linéaire et généralement non-stationnaire. La modélisation du comportement pouvant être traitée de manière purement phénoménologique ou en lien avec les travaux du thème « mécanique des milieux hétérogènes et homogénéisation ». Les applications visées vont du nucléaire à l’aéronautique en passant par le transport et la mise en œuvre de matériaux. Les questions scientifiques abordées ont principalement un lien avec la tenue et la durée de vie de structures en prenant en compte leur environnement (fatigue, vieillissement, fluage, endommagement/guérison, etc). 

Aspects numériques et logiciels

Les problématiques multiphysiques nous amènent à développer des formulations numériques spécifiques (par exemple : espace-temps isogeométrique ou multi-grilles) qui peuvent permettre de traiter certains verrous numériques (par exemple liés aux échelles de temps propres à chaque physique). Ces développements peuvent se décliner sur le plan logiciel dans des outils propres, i.e. des codes éléments-finis internes, ou des outils développés par un partenaire industriel ou encore dans des codes commerciaux (comme Abaqus par exemple).    

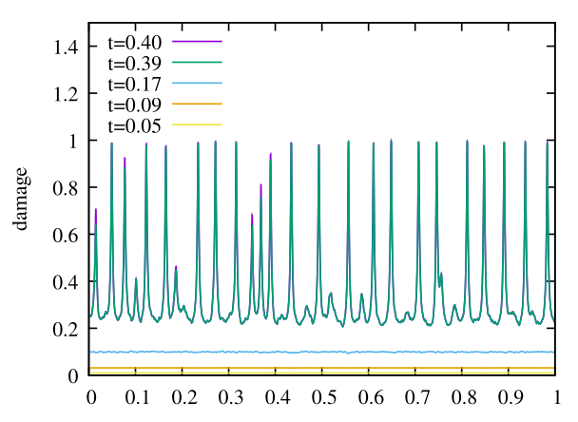Figure 3: Multi-fissuration d'une barre élastique fragile soumisse à une explosion. Résolue avec une méthode espace-temps isogéométrique en Galerkin discontinu avec une formulation en champs de phase.