Propagation en milieux microstructurés

L’hypothèse de périodicité du milieu donne accès à l’outil d’analyse des ondes de Bloch, très largement utilisé dans la communauté (métamatériaux notamment). L’analyse des modèles périodiques fait partie des outils de base des chercheurs travaillant dans cette thématique, et continuera à être utilisée et développée dans les prochaines années en fonction des besoins. Les spécificités de l’équipe sur cette sous-thématique concernent l’utilisation combinée de l’analyse périodique avec les outils d’analyse asymptotique (dynamique effective de milieux périodiques: homogénéisation de volume ou de surface à fort contraste, homogénéisation d’ordre 2 et lien avec la mécanique des milieux continus généralisée), le travail en haute fréquence (courbes de dispersion de Bloch au voisinage des frontières de Brillouin pour les milieux périodiques), le développement de modèles spécifiques pour certaines applications (par exemple prise en compte de l’influence de l’interface agrégat-matrice dans les bétons), ainsi que la volonté de construire des modèles macroscopiques (EDP, lois de contact) bien posés mathématiquement et bien adaptés au calcul numérique.

Légende : (a) courbes de dispersion et (b) champ de vitesses instantané dans un trilaminé 1D, et dans les modèles homogénéisés correspondants : Cauchy et à gradient de contraintes. Travail de post-doctorat de Logan Schwann.

Ce domaine de recherche se concentre sur l'étude théorique et expérimentale de la propagation dans des matériaux poro-élastiques. Les modèles développés intègrent des concepts avancés tels que l'aspect fractal des pores, l'interaction visco-thermique entre fluide et structure, ainsi que l'utilisation du calcul fractionnaire pour décrire la dispersion temporelle et spatiale. De plus, les effets micropolaires sont également pris en compte dans la modélisation, en accord avec une observation expérimentale de l'interaction onde/matière.

Pour caractériser ces milieux, une approche inverse est adoptée, reposant sur des mesures expérimentales ou simulées de champs acoustiques, sans linéarisation des équations du modèle mathématique sous-jacent. Une attention particulière est accordée à la sélection de modèles-estimateurs pertinents, en tenant compte de l'influence des erreurs sur les reconstructions.

Dans une perspective de développement durable, des études sont menées sur la caractérisation des blocs de terre comprimés pour la construction de maisons écologiques, ainsi que sur la caractérisation ultrasonore et vibratoire des films minces.

Légende : Elastic Vibration of a Micropolar Plate

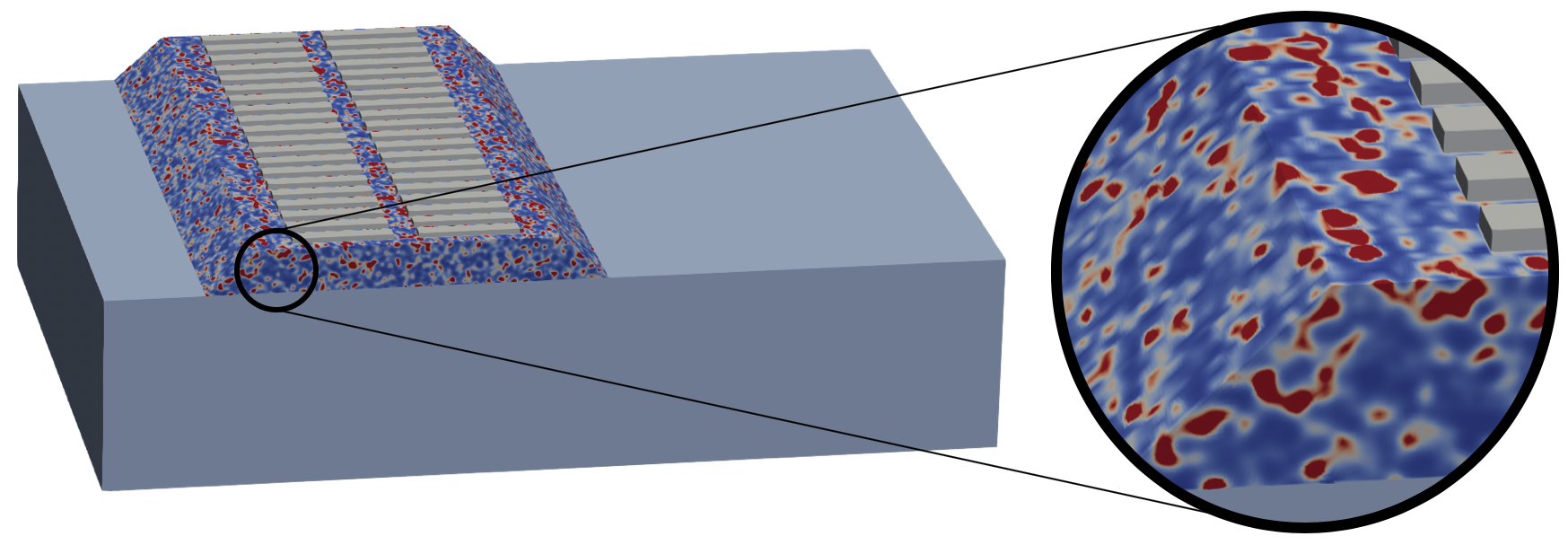
La modélisation probabiliste des milieux hétérogènes permet de représenter des fluctuations réalistes de propriétés qui ne peuvent l’être par des modèles périodiques ou fractals. Elle est en particulier utilisée au laboratoire pour obtenir des modèles asymptotiques pour les amplitudes des champs d’ondes à grande distance de propagation : équation de transfert radiatif, équation de diffusion, équations différentielles stochastiques en milieu stratifié. Ces approches théoriques peuvent servir à développer des méthodes expérimentales pour l’imagerie par ultrasons de milieux très hétérogènes (béton, cellules sanguines en écoulement), l’imagerie à travers des réseaux de fissures, ou l’imagerie d’objets ou de défauts au sein de tels milieux. Enfin, des comportements spécifiques aux milieux aléatoires, n’apparaissant pas dans les milieux périodiques, comme la localisation d’Anderson, peuvent être compris et utilisés (par exemple pour l’isolation acoustique ou vibratoire) dans le cadre d’un formalisme aléatoire.

Légende : (a) partie d’un modèle numérique de voie ferroviaire ballastée, et champ de déplacement en bord de voie à différentes positions longitudinales pour un modèle de ballast (b) homogène ou (c) hétérogène. Travail de doctorat de Patryk Dec.