Waves propagation in microstructured materials

The assumption of periodicity of the medium gives access to the Bloch wave analysis tool, widely used in the community (metamaterials in particular). The analysis of periodic models is one of the basic tools used by researchers working in this field, and will continue to be used and developed in the coming years as needs arise. The team's specific features in this sub-theme concern the combined use of periodic analysis with asymptotic analysis tools (effective dynamics of periodic media: high-contrast volume or surface homogenization, second-order homogenization and link with generalized continuum mechanics), high-frequency work (Bloch dispersion curves near Brillouin boundaries for periodic media), the development of specific models for certain applications (e.g. taking into account the influence of the aggregate-matrix interface in concrete), and the desire to build macroscopic models (PDEs, contact laws) that are mathematically well-posed and well-suited to numerical computation.

Legend: (a) dispersion curves and (b) instantaneous velocity field in a 1D trilaminate, and in the corresponding homogenized models: Cauchy and stress gradient. Logan Schwann's post-doctoral work.

This area of research focuses on the theoretical and experimental study of propagation in poro-elastic materials. The models developed incorporate advanced concepts such as the fractal aspect of pores, visco-thermal interaction between fluid and structure, and the use of fractional calculus to describe temporal and spatial dispersion. In addition, micropolar effects are also taken into account in the modeling, in line with experimental observation of wave/matter interaction.

To characterize these media, an inverse approach is adopted, based on experimental or simulated measurements of acoustic fields, without linearization of the underlying mathematical model equations. Particular attention is paid to the selection of relevant model-estimators, taking into account the influence of errors on reconstructions.

With a view to sustainable development, studies are being carried out on the characterization of compressed earth blocks for the construction of ecological houses, as well as on the ultrasonic and vibratory characterization of thin films.

Legend : Elastic Vibration of a Micropolar Plate

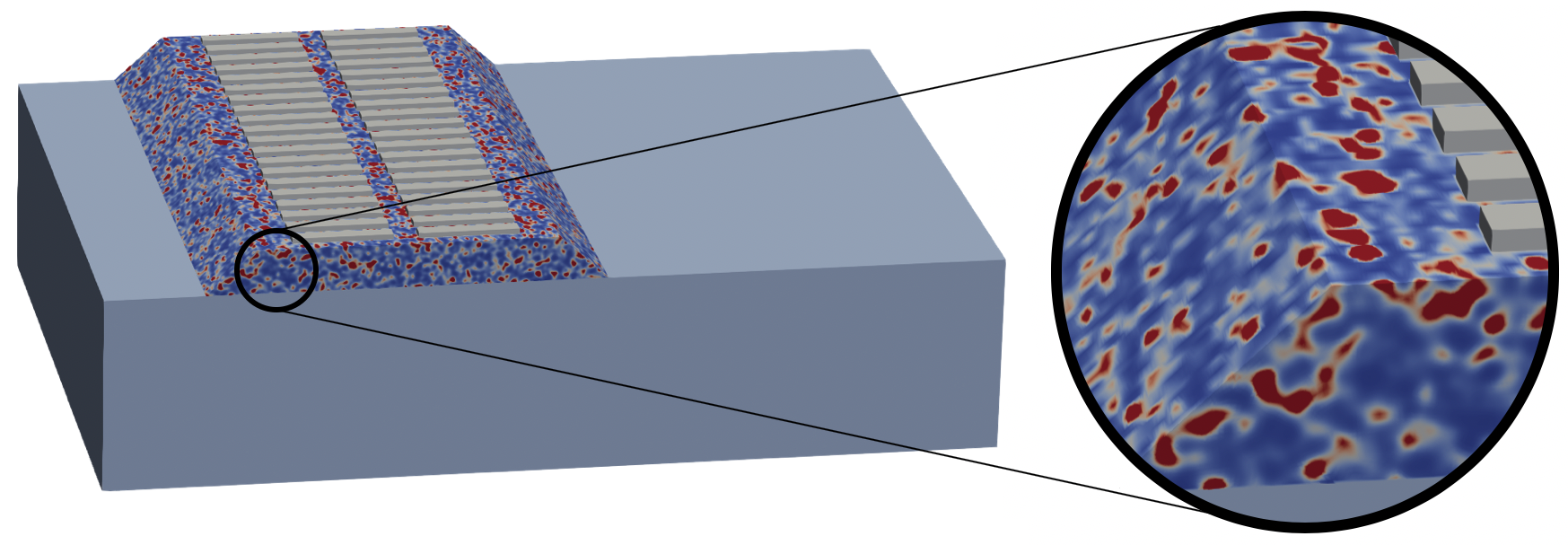
Probabilistic modeling of heterogeneous media makes it possible to represent realistic fluctuations in properties that cannot be represented by periodic or fractal models. In particular, it is used in the laboratory to obtain asymptotic models for wave field amplitudes at long propagation distances: radiative transfer equation, diffusion equation, stochastic differential equations in stratified media. These theoretical approaches can be used to develop experimental methods for ultrasound imaging of highly heterogeneous media (concrete, flowing blood cells), imaging through crack networks, or imaging objects or defects within such media. Finally, behaviors specific to random media, which do not appear in periodic media, such as Anderson localization, can be understood and used (e.g. for acoustic or vibration isolation) within the framework of a random formalism.

Legend: (a) part of a numerical model of a ballasted railway track, and trackside displacement field at different longitudinal positions for a (b) homogeneous or (c) heterogeneous ballast model. PhD work by Patryk Dec.