Propagation non linéaire
Les recherches liées à la propagation des ondes non linéaires se déclinent selon deux directions. Le dénominateur commun de ces travaux est le formalisme des systèmes hyperboliques non linéaires.
Participants permanents : B. Lombard (DR), R. Saurel (Prof AMU)
Thermodynamique, ondes et milieux hors d'équilibre
Dans de nombreuses applications la thermodynamique du milieu en écoulement est gouvernée par une équation d’état complexe. Parfois les critères de convexité ne sont pas satisfaits dans tout l’espace des phases, ce qui conduit à des échecs des simulations ou à l’emploi de méthodes de prolongement contenant un certain caractère arbitraire. Certaines équations d’état ont un domaine de validité restreint, ce qui est problématique dans les simulations où les variables d’écoulement ont un domaine de variation arbitraire. Enfin, ces équations d’état induisent aussi un coût de calcul élevé. Dans le contexte des modèles multiphasiques à relaxation, la majeure partie du temps de calcul est passé dans les modules de calcul de thermodynamique.
Ce type de problématique se rencontre dans de nombreuses applications :
-
En présence de transition de phase.
-
En combustion de matériaux énergétiques condensés et en particulier pour les ondes de détonation, extrêmement non linéaires.
Des travaux sont promus actuellement afin d’aborder ces problèmes de thermodynamique au moyen d’une approche innovante, basée sur une méthode de relaxation. Une équation d’état ‘prédicteur’ est employée dans le solveur d’écoulement. Celle-ci est convexe, simple et rapide. Ses paramètres sont transportés dans l’écoulement au moyen d’équations de transport avec relaxation. A la fin de pas de temps, ces paramètres sont relaxés vers ceux de la véritable équation d’état, lorsque les domaines de validité et de convexité sont respectés. Lorsqu’un des critères n’est pas respecté, la simulation se poursuit avec les derniers paramètres transportés, ce qui consiste en un prolongement automatique de l’équation d’état. Cette méthode est en cours de validation et extension à différents domaines de la physique. Pour l’instant, les gains enregistrés sont conséquents, autant en termes de robustesse que de rapidité.
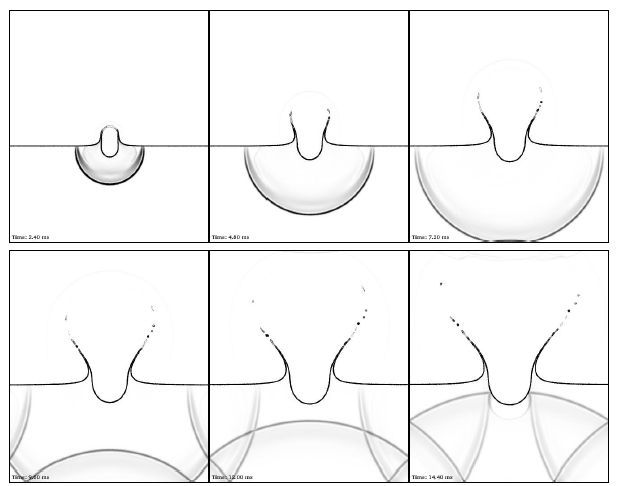
Simulation 2D d'une explosion sous-marine proche de la surface atmosphérique. Les isocontours de fraction volumique du liquide sont représentés à 6 instants successifs. La méthode de relaxation thermodynamique est employée dans une méthode de capture d'interfaces diffuses. Un gain en temps calcul d'un facteur 6 est obtenu par rapport à l'emploi de l'équation d'état conventionnelle
Ondes guidées, homogénéisation et nonlinéarités
La propagation d’ondes linéaires dans des milieux périodiques conduit à des comportements bien connus maintenant, tels que l’existence de bandes de fréquence interdite et de modes protégés topologiquement. Les outils classiques pour étudier ces phénomènes sont l’homogénéisation et l’analyse de Floquet-Bloch. Lorsque des nonlinéarités interviennent, liées à des déformations finies ou des lois de comportement, de nouveaux phénomènes sont attendus, nécessitant de nouveaux outils théoriques et numériques.
L'équation de Sine-Gordon est l'archétype de l'équation des ondes non linéaires : à l'équation de d'Alembert est ajouté un simple terme sinusoïdal. Cette équation prototype décrit de nombreuses situations physiques, du mouvement d'un pendule de torsion à la dynamique d'un brin d'ADN. Malgré sa simplicité, cette équation conduit à de nombreuses questions encore ouvertes. Dans un travail publié en 2024, la stabilité des solutions périodiques a été analysée par la méthode des équations de modulation de Whitham. Un temps d’explosion de la solution (apparition d’une caustique) a été déterminé théoriquement et comparé à des simulations numériques (cf. figure ci-dessous).
Un autre exemple d’onde guidée non linéaire est donné par l’écoulement d’un fluide en eau peu profonde. La hauteur des vagues est décrite par l’équation de Korteweg-de Vries, bien connue en hydrodynamique, et qui conduit à l’existence de solitons. Lorsque la topographie présente un obstacle (marche, trou, etc), des solutions périodiques stationnaires peuvent être générées par l’écoulement. Un travail en cours, mené conjointement par des chercheurs des équipes OI et de Sons, porte sur l’étude théorique et numérique de ces ondes. Cette étude permet une analogie avec des équations décrivant la physique des trous noirs, notamment le rayonnement de Hawking.
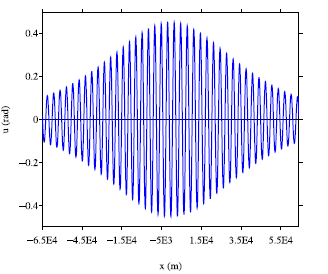
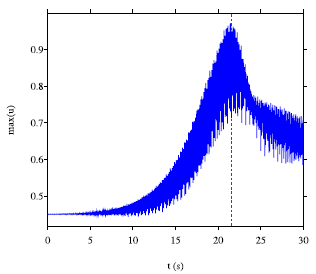
Sine-Gordon à coefficients périodiques. Gauche : solution périodique modulée, à l’instant d’origine. Droite : évolution de l’énergie, et comparaison avec le temps d’explosion théorique de la solution (trait vertical pointillé)