Nonlinear waves propagation

Research into the propagation of nonlinear waves has two main thrusts. The common denominator is the formalism of nonlinear hyperbolic systems.

Permanent members : B. Lombert (DR), R. Saurel (Prof AMU)

Thermodynamics, waves and non-equilibrium media

In many applications, the thermodynamics of the flowing medium is governed by a complex equation of state. Sometimes the convexity criteria are not satisfied throughout the phase space, leading to failed simulations or the use of extension methods containing a certain arbitrariness. Some equations of state have a restricted domain of validity, which is problematic in simulations where the flow variables have an arbitrary range of variation. Finally, these equations of state also entail a high computational cost. In the context of multiphase relaxation models, most of the computation time is spent in the thermodynamics calculation modules.

This type of problem is encountered in many applications:

Work is currently being promoted to tackle these thermodynamic problems using an innovative approach based on a relaxation method. A 'predictor' equation of state is used in the flow solver. It is convex, simple and fast. Its parameters are transported in the flow by means of transport equations with relaxation. At the end of each time step, these parameters are relaxed to those of the true equation of state, when the validity and convexity domains are respected. When one of the criteria is not met, the simulation continues with the last transported parameters, automatically extending the equation of state. This method is currently being validated and extended to various fields of physics. For the time being, the gains recorded are substantial, both in terms of robustness and speed.

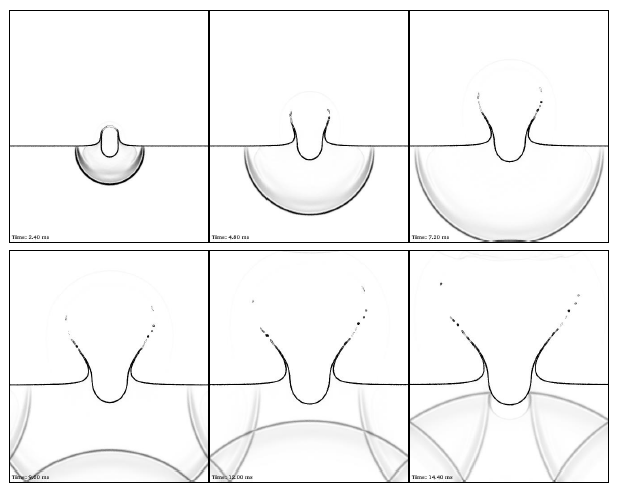
2D simulation of an underwater explosion near the atmospheric surface. Liquid volume fraction isocontours are plotted at 6 successive instants. The thermodynamic relaxation method is used in a method for capturing diffuse interfaces. Computational time savings of a factor of 6 are obtained compared to the use of the conventional equation of state

Guided waves, homogenization and nonlinearities

Linear wave propagation in periodic media leads to behaviors that are now well known, such as the existence of forbidden frequency bands and topologically protected modes. The classical tools for studying these phenomena are homogenization and Floquet-Bloch analysis. When nonlinearities are involved, linked to finite deformations or behavior laws, new phenomena are expected, requiring new theoretical and numerical tools.

The Sine-Gordon equation is the archetypal non-linear wave equation: a simple sinusoidal term is added to the d'Alembert equation. This prototype equation describes many physical situations, from the motion of a torsion pendulum to the dynamics of a DNA strand. Despite its simplicity, this equation leads to many open questions. In a work published in 2024, the stability of periodic solutions was analyzed using the Whitham modulation equation method. A solution explosion time (appearance of a caustic) was determined theoretically and compared with numerical simulations (see figure below).

 Another example of a non-linear guided wave is the flow of a fluid in shallow water. The wave height is described by the Korteweg-de Vries equation, well known in hydrodynamics, and which leads to the existence of solitons. When the topography presents an obstacle (step, hole, etc.), stationary periodic solutions can be generated by the flow. Ongoing work, carried out jointly by researchers from the Waves and Imaging and Sounds teams, focuses on the theoretical and numerical study of these waves. This study provides an analogy with equations describing the physics of black holes, notably Hawking radiation.

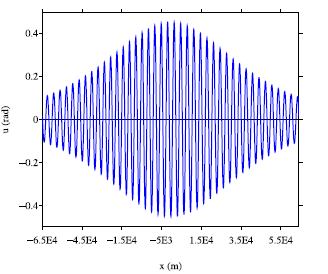
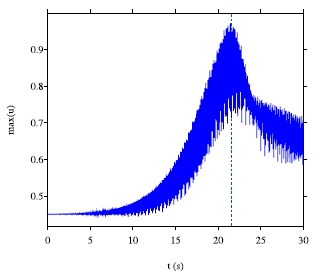
Sine-Gordon with periodic coefficients. Left: modulated periodic solution, at the original instant. Right: energy evolution, and comparison with the theoretical explosion time of the solution (dotted vertical line).